

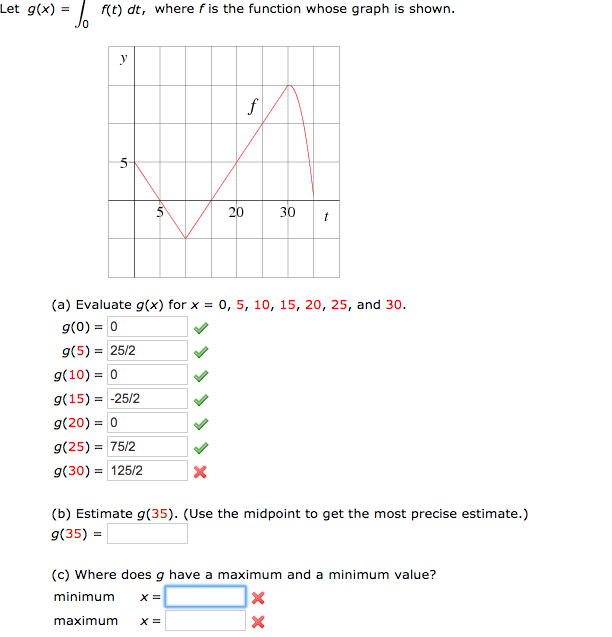
The question is: Xf/Xp>(Xf+Yf)/(Xp+Yp)? to be true) Since Full-time employees of company Z: Xf+Yf More than half of the full-time employees of Company Z are employees of division X, and more than half of the part-time employees of Company Z are employees of division Y. 4 The recursive call passes Cons(y, yf ) rather than xf (), which denotes. The ratio of the number of full-time employees to the number of part-time employees is less for division Y than for Company Z For a contrived demonstration of constant functions, let us compute the prod. If each division has some part-time employees, is the ratio of the number of full-time employees to the number of part-time employees greater for division X than for Company Z? Translate an object by Adding translation distances to coordinates to generate new coordinates positions Let,(x, y) be the 2-D point and tx, ty be the translation distance, we have In matrix format, where T is the translation vector 5By: Tekendra Nath Yogi xtx'x yty'y y x P y x t t T 'y 'x 'P TP'P Translating a point from. Each employee of Company Z is an employee of either division X or division Y, but not both. => 12(x+1)(3x+2) is divisible by 24, thus the remainder is zero.Ģ.

I have written a condition if simulationArea. Now coming to an important point which is what I did. Here X and Y are coordinates after touchstart or mouse start ie Mouseclick or Touch on-screen on simulation area.
If c=2 then n=2x+1 and n= 3y+2 => n=6x+5. Xf and Xf are the hover coordinates of the mouse before the click, which was originally passed on the hover function for circuit elements. => 12x(3x+1) is divisible by 24, thus the remainder is zero.Ģ. Thus every power of 2 is an element of S. Now n¡1 2
S=Ax+B, where A is the dividing number (constant numbers), and B is the remainder.Ī is the least multiple of A1 and A2 B is the least possible value of S that let S1=S2. General term is usually in the following form: To solve such questions, firstly, we must prove some support law for general term of divisible numbers. This is one of the most tricky questions in GMATPrep. If n is a positive integer and r is the remainder when (n-1)(n+1) is divided by 24, what is the value of r? If XF 71 and YF 20, Find XY2.If XY4Y-1, YF8, and XF9Y-23 find the value of Y3.If XF85, XY5c-9, and YF2C+10 find YF4.If XY4X+10, YF2X-1, and XF9X-15, find XF( show the work if you can) Categories Uncategorized.
#Let xf and yf be adjacent full
Users should refer to the original published version of the material for the full abstract.The following is list of some tricky math questions, which are in GMATPrep, collected by me during study.ġ. If XF 71 and YF 20, Find XY2.If XY4Y-1, YF8, and XF9Y-23 find the value. No warranty is given about the accuracy of the copy. However, users may print, download, or email articles for individual use.
#Let xf and yf be adjacent free
If M is either a free module with rank(M) ≥ 2 or a non-finitely generated projective module there exists f € M* with rad(Γf(M)) = 1 and diam(Γf(M)) ≤ 2. In this case lim z - yf (x)-xf (y) y-x + z f (y)-f (x) y-x +, and, thanks to the result of the previous question we conclude that f is not bounded. Also if Γf(M) = ∅, then f is monomorphism (the converse is true if R is a domain). Furthermore if |Γf(M)| ≥ 1, then Γf(M) is finite if and only if M is finite. Moreover, if Γf(M) contains a cycle, then (Γf(M)) ≤ 4. We observe that over a commutative ring R, Γf(M) is connected and diam(Γf(M)) ≤ 3. We associate an undirected graph Γf(M) to M in which non-zero elements x and y of M are adjacent provided that xf(y) = 0 or yf(x) = 0. Abstract: Let M be an R-module and 0 ≠ f € M* = Hom(M, R).


 0 kommentar(er)
0 kommentar(er)
